Mo logo [home] [lexicon] [problems] [tests] [courses] [auxiliaries] [notes] [staff] german flag
Mathematik-Online lexicon:

Real Fourier-Series

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z overview
We determine the real Fourier series of the $ 2\pi$-periodic extension of the function depicted in the figure.

\includegraphics[clip,width=.9\linewidth]{b_fourier_reihe_f}

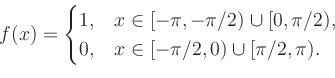
\begin{displaymath} f(x)= \begin{cases} 1, & x\in[-\pi,-\pi/2)\cup[0,\pi/2), \\ 0, & x\in[-\pi/2,0)\cup[\pi/2,\pi). \end{cases}\end{displaymath}

(i) Cosine coefficients:

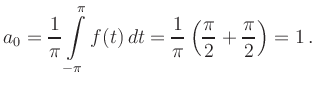
$\displaystyle a_0 = \frac{1}{\pi} \int\limits_{-\pi}^\pi f(t)\,dt = \frac{1}{\pi}\left( \frac{\pi}{2}+\frac{\pi}{2}\right) = 1 \,. $

For $ k\ge 1$ we obtain, using that cosine is an odd function,
$\displaystyle a_k$ $\displaystyle =$ $\displaystyle \frac{1}{\pi} \left( \int\limits_{-\pi}^{-\pi/2}\cos(kt)\,dt + \i... ...i/2}\cos(kt)\,dt \right) = \frac{1}{\pi} \int\limits_0^\pi \cos(kt)\,dt = 0 \,.$  

(ii) Sine coefficients:

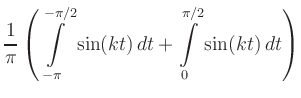$\displaystyle b_k$ $\displaystyle =$ $\displaystyle \frac{1}{\pi} \left( \int\limits_{-\pi}^{-\pi/2}\sin(kt)\,dt + \int\limits_0^{\pi/2}\sin(kt)\,dt \right)$  
  $\displaystyle =$ $\displaystyle \frac{1}{\pi} \left( \left[ -\frac{\cos(kt)}{k}\right]_{-\pi}^{-\pi/2} +\left[ -\frac{\cos(kt)}{k}\right]_0^{\pi/2} \right)$  
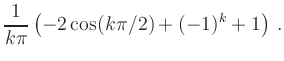  $\displaystyle =$ $\displaystyle \frac{1}{k\pi} \left(-2\cos(k\pi/2)+(-1)^k+1\right) \,.$  

Depending on whether $ \cos(k\pi/2)$ equals 0, $ 1$ or $ -1$, we distinguish $ 3$ cases:
$ k$ odd: $ b_k =0$,
$ k=4m$: $ b_{4m} =0$,
$ k=4m+2$: $ b_{4m+2}=4/((4m+2)\pi)$.

(iii) Fourier series of $ f$:

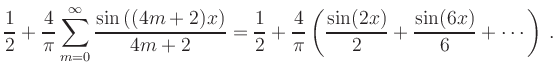
$\displaystyle \frac{1}{2}+\frac{4}{\pi}\sum_{m=0}^\infty \frac{\sin\left((4m+2... ...\frac{4}{\pi}\left(\frac{\sin(2x)}{2} + \frac{\sin(6x)}{6} + \cdots\right) \,. $

The figure shows the partial sums

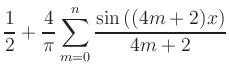
$\displaystyle \frac{1}{2} +\frac{4}{\pi}\sum\limits_{m=0}^n \frac{\sin\left((4m+2)x\right)}{4m+2} $

for $ n=2$ and $ n=8$.

\includegraphics[clip,width=.9\linewidth]{b_fourier_reihe_f_p1_p8}

Since $ f$ is not continuous, the convergence of the Fourier series is very slow. We notice oscillations in the vicinity of the jump discontinuities, which is referred to as Gibb's phenomenon.

see also:

  automatisch erstellt am 22.  9. 2016