

Mathematik-Online lexicon:

|
[home] [lexicon] [problems] [tests] [courses] [auxiliaries] [notes] [staff] |

|
|
Mathematik-Online lexicon: | ||
Curve Sketching of a Periodic Function | ||
| A B C D E F G H I J K L M N O P Q R S T U V W X Y Z | overview |
Symmetry:
Since
![]() , the function is odd.
, the function is odd.
Periodicity:
As the sine function, the function is ![]() -periodic.
Hence, it is sufficient to consider the interval
-periodic.
Hence, it is sufficient to consider the interval
![]() .
.
Points of discontinuity and Poles: The function is a composition of continuous functions, and, therefore, has no points of discontinuity or poles.
Zeros:
By the addition theorem,
![]() ,
and it follows that
,
and it follows that
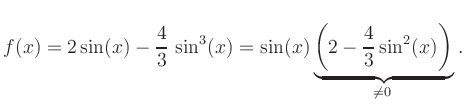
Extrema: The derivative

Inflection Points: The second derivative
Asymptots:
Since ![]() is periodic and not constant, it has no asymptotes.
is periodic and not constant, it has no asymptotes.
![\includegraphics[width=10.4cm]{Kurvendiskussion_1_en}](/inhalt/beispiel/beispiel45/img28.png)
| automatisch erstellt am 22. 6. 2016 |