Mo logo [home] [lexicon] [problems] [tests] [courses] [auxiliaries] [notes] [staff] german flag
Mathematik-Online lexicon:

4-point scheme

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z overview

Cubic interpolation is frequently used to fit data $ f_k$ at equally spaced points $ x_k=kh$, in particular, for plotting the graph of an interpolating function $ f$. Intermediate values at the midpoints $ x_{k+1/2}=(k+1/2)h$ are approximated by a weighted sum of neighboring data:

$\displaystyle f_{k+1/2} = (-f_{k-1}+9f_k+9f_{k+1}-f_{k+2})/16 \,. $

This process is repeated until sufficiently many values are generated. The weights

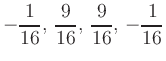
$\displaystyle -\frac{1}{16},\, \frac{9}{16},\, \frac{9}{16},\, -\frac{1}{16} $

of this $ 4$-point-rule are the values of the Lagrange polynomials at the point $ x_{k+1/2}$. For example,

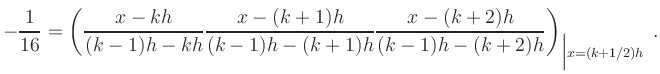
$\displaystyle -\frac{1}{16} = \left( \frac{x-kh}{(k-1)h-kh} \frac{x-(k+1)h}{(... ...h-(k+1)h} \frac{x-(k+2)h}{(k-1)h-(k+2)h} \right)_{\Big\vert x = (k+1/2)h} \,. $

In view of symmetry, and since the weights sum to one (interpolation of constant data), the other weights can be determined without further computation.

\includegraphics[width=.45\textwidth]{KubischeInterpolation_Bild1} \includegraphics[width=.45\textwidth]{KubischeInterpolation_Bild2}
\includegraphics[width=.45\textwidth]{KubischeInterpolation_Bild3} \includegraphics[width=.45\textwidth]{KubischeInterpolation_Bild4}

The figure shows a three-fold application of $ 4$-point-interpolation to data of a sine function. While the limit function, shown on the left part of the figure, appears to be smooth, merely the first derivative is continuous.

\includegraphics[width=.4\textwidth]{fourpoint_lim}          \includegraphics[width=.4\textwidth]{fourpoint_diff}

The right part of the figure shows an approximation of the second derivative via divided differences after $ 8$-fold interpolation. Apparently, the graph has a fractal character.

see also:

  automatisch erstellt am 22.  6. 2016