Mathematics-Online lexicon: Cyclic Codes

	[home] [lexicon] [problems] [tests] [courses] [auxiliaries] [notes] [staff]
	Mathematics-Online lexicon:
	Cyclic Codes

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z

overview

Generating Polynomials

In the following let $\mbox{$q=p^f$}$ be a prime power and $\mbox{$\mathbb{F}_q$}$ denotes the field with $\mbox{$q$}$ elements.

A linear code $\mbox{$C\subset\mathbb{F}_q^N$}$ is called cyclic, if

$\mbox{$\displaystyle (c_0,\dots,c_{N-1})\in C\;\Rightarrow\;(c_{N-1},c_0,c_1,\dots,c_{N-2})\in C. $}$

A cyclic code is described by an ideal in $\mbox{$R:=\mathbb{F}_q[X]/(X^N-1)\mathbb{F}_q[X]$}$ ; each code word $\mbox{$c=(c_0,\dots, c_{N-1})\in\mathbb{F}_q^N$}$ is identified with

$\mbox{$\displaystyle (c_0,c_1,\dots,c_{N-1})= c_0 + c_1 X + \dots+c_{N-1}X^{N-1}\in R $}$

Note that is not a field because is not irreducible. Assume from now on that $\mbox{$N$}$ is not divisible by $\mbox{$p$}$ . Starting with a factorization

$\mbox{$\displaystyle X^N-1 = f_{(1)}(X)\cdot \ldots \cdot f_{(t)}(X) \in \mathbb{F}_q[X] $}$

in pairwise different, normalized and irreducible polynomials $\mbox{$f_{(i)}\in\mathbb{F}_q[X]$}$ , the ideals of $\mbox{$R$}$ have the form

$\mbox{$\displaystyle f_{(i_1)}\cdot \ldots \cdot f_{(i_s)}R, $}$

where $\mbox{$0\leq s\leq t$}$ and $\mbox{$1\leq i_1<i_2<\dots<i_s\leq t$}$ .

Such a polynomial $\mbox{$g:=f_{(i_1)}\cdots f_{(i_s)}=\sum_{j=0}^{N-k}g_jX^j$}$ of degree $\mbox{$N-k$}$ is called a generator polynomial of the cyclic code $\mbox{$C_g:=gR\subseteq R$}$ of dimension $\mbox{$k$}$ . A generator matrix is

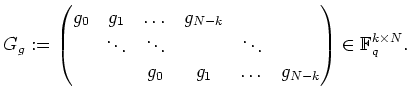
$\mbox{$\displaystyle G_g:=\begin{pmatrix} g_0 & g_1 & \dots & g_{N-k} & \\ ... ... & & g_0 & g_1 & \dots & g_{N-k} \end{pmatrix}\in\mathbb{F}_q^{k\times N}. $}$

The polynomial $\mbox{$h=\sum_{j=0}^{k}h_j X^j\in\mathbb{F}_p[X]$}$ with $\mbox{$gh=X^N-1$}$ is called check polynomial of $\mbox{$C_g$}$ . A parity check matrix is given by

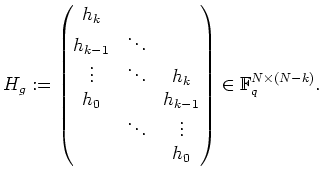
$\mbox{$\displaystyle H_g:=\begin{pmatrix} h_k & & \\ h_{k-1} & \ddots & \... ...& \ddots & \vdots \\ & & h_0 \end{pmatrix}\in\mathbb{F}_q^{N\times(N-k)}. $}$

Minimal Distance in Cyclic Codes

The minimal distance of cyclic codes is in general difficult to determine. The following estimation is known.

Let $\varphi$ be the Euler $\varphi$ - function, i.e. $\mbox{$\varphi(N)$}$ denotes the number of $n \in \{1,\dots,N\}$ which do not divide .

If $\mbox{$\alpha$}$ is a zero of $\mbox{$X^N-1\in\mathbb{F}_q[X]$}$ in $\mbox{$\mathbb{F}_{q^{\varphi(N)}}$}$ with $\mbox{$N=\min\{n\in\mathbb{N}:\alpha^n=1\}$}$ , then $\mbox{$\alpha$}$ is called a primitive $\mbox{$N$}$ -th root of unity over $\mbox{$\mathbb{F}_q$}$ .

Let $\mbox{$C_g \subseteq R$}$ be a cyclic code and $\alpha$ a primitive $\mbox{$N$}$ -th root of unity. If $\mbox{$g(\alpha^b)=0, g(\alpha^{b+1})=0, \dots, g(\alpha^{b+\delta-2})=0$}$ for each choice of $\mbox{$b\in\mathbb{N}$}$ , $\mbox{$\delta \geq 2$}$ then $\mbox{$d(C_g) \geq \delta$}$ .

Coding with Cyclic Codes

Let $\mbox{$C_g$}$ be a cyclic code with $\mbox{$g=\sum_{j=0}^{N-k}g_jX^j$}$ , length $\mbox{$N$}$ and dimension $\mbox{$k$}$ . In order to find for a given information word $\mbox{$u=(u_0,\dots,u_{k-1})\in\mathbb{F}_q^k$}$ a code word $\mbox{$c=(c_0,\dots, c_{N-1})\in\mathbb{F}_q^N$}$ , controlbits are calculated with the aid of polynomial division. For this the information word is first written as an element of $\mbox{$\mathbb{F}_q[X]$}$ .

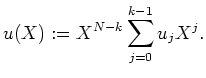
$\mbox{$\displaystyle u(X) := X^{N-k} \sum_{j=0}^{k-1} u_jX^j. $}$

Polynomial division of $\mbox{$u(X)$}$ through $\mbox{$g(X)$}$ yields the residue

$\mbox{$\displaystyle r(X)=\sum_{j=0}^{N-k-1}r_jX^j\in\mathbb{F}_q[X]$}$

Now the code word to the given information word is

$\mbox{$\displaystyle c = (-r_0,\dots,-r_{N-k-1},u_0,\dots,u_{k-1})$}$

()

see also:

[Examples]

automatically generated 7/14/2005