Mo logo [home] [lexicon] [problems] [tests] [courses] [auxiliaries] [notes] [staff] german flag
Mathematics-Online lexicon:

Codes and Linear Codes

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z overview

Codes.

Let $ \mbox{$A$}$ be a finite set with $ q \geq 2 $ elements, which is called alphabet. A code $ \mbox{$C$}$ of length $ \mbox{$N\geq 1$}$ is a subset of $ \mbox{$A^N$}$. The code words are written as $ N$ - tuples

$\displaystyle (x_1, \ldots , x_N) , \ \ x_i \in A .$

The information rate of $ \mbox{$C$}$ is defined as

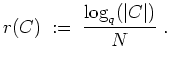
$ \mbox{$\displaystyle r(C) \;:=\; \frac{\log_q(\vert C\vert)}{N}\;. $}$

For $ \mbox{$x,y\in A^N$}$ the Hamming distance of $ \mbox{$x=(x_1,\dots,x_N)$}$ and $ \mbox{$y=(y_1,\dots,y_N)$}$ is

$ \mbox{$\displaystyle d(x,y) \;:=\; \vert\{i\in\{1,\dots,N\}\;:\;x_i \neq y_i\}\vert\;. $}$
The minimal distance between two different words in $ \mbox{$C$}$ is called minimal distance $ \mbox{$d(C)$}$ of $ \mbox{$C$}$.

A minimal distance decoder (MDD) gives to each $ \mbox{$a\in A^N$}$ a word $ \mbox{$c\in C$}$, which has minimal Hamming distance to $ a .$ A MDD is therefore a function $ \mbox{$f:A^N\longrightarrow C$}$ with

$ \mbox{$\displaystyle d(f(a),a) = \min\{d(c,a):c\in C\} $}$
for all $ \mbox{$a\in A^N$}$.

Two codes $ \mbox{$C$}$ and $ \mbox{$C'$}$ are called equivalent provided there is a permutation $ \mbox{$\sigma$}$ of $ \mbox{$\{1,\dots,N\}$}$ such that

$ \mbox{$\displaystyle c = (c_1,\dots,c_N) \mapsto (c_{\sigma(1)}, \dots,c_{\sigma(N)})$}$
is a bijection from $ \mbox{$C$}$ to $ \mbox{$C'$}$. . Equivalent codes have the same information rate and the same minimal distance.

Task of coding theory is to find codes with big minimal distance and big information rate.

Linear Codes.

Let $ \mbox{$A=\mathbb{F}_{p^l}$}$ be a finite field and $ \mbox{$A^N$}$ the vector space of dimension $ \mbox{$N$}$ over $ \mbox{$A$}$. A subspace $ \mbox{$C$}$ of $ \mbox{$A^N$}$ is called a linear code. If $ \mbox{$(b_1,\dots,b_k)$}$ is a basis of $ \mbox{$C$}$, written as row vectors,then the matrix $ \mbox{$B\in A^{k\times N}$}$ with the rows $ \mbox{$b_1,\dots,b_k$}$ is called a generator matrix of $ \mbox{$C$}$.

A linear code $ \mbox{$C\subseteq A^N$}$ of dimension $ \mbox{$k$}$ has the information rate $ \mbox{$r(C) = \frac{k}{N}$}$. If its minimal distance is $ \mbox{$d=d(C)$}$, then the code is called a $ \mbox{$[N,k,d]$}$-Code.

The minimal distance of a linear code coincides with the minimal number of non-zero entries of a code word which is different from the zero vector.

Let $ F$ be a finite field and let $ C \subset F^N$ be a code. Assume that any two distinct words of $ C$ have distance at least $ 2f + 1$, i.e. $ d(C) \geq 2f + 1. $ Suppose that $ y \in F^n$ differs from a code word $ x$ by $ t \leq f$ coordinates (if $ y$ is the word obtained after transmission of $ x$ then one says the transmission had $ t$ errors ). Because $ d(C) \geq 2f +1 $ all other code words differ from $ y$ by more than $ f$ coordinates. So we have a unique candidate which code word $ y$ should be if it is obtained after transmission of some code word. Note that the correction of $ y$ to this candidate is correct provided the transmission had no more than $ f$ errors. This leads to the following definition.

An $ f$ - error correcting code is a subset of $ F^N$ with the property

$\displaystyle \forall_{x \in C} \forall_{a \in C} \ \ x \neq a \ \Longrightarrow \ d(x,a) \geq 2f + 1 .$

Let $ \mbox{$C$}$ be a linear code of dimension $ \mbox{$k$}$, then $ \mbox{$C$}$ is equivalent to a linear code with a generator matrix $ \mbox{$(E_k\vert P_{N-k})$}$, where $ \mbox{$E_k\in A^{k\times k}$}$ denotes the identity matrix.

For a linear code $ \mbox{$C$}$ with generator matrix $ \mbox{$G =(E_k\vert P_{N-k})\in A^{k\times N}$}$ a check matrix is given by

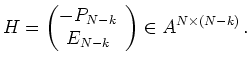
$ \mbox{$\displaystyle H=\left(\begin{matrix}-P_{N-k}\\ E_{N-k}\end{matrtix}\right)\in A^{N\times(N-k)}\, .$}$

Each matrix $ \mbox{$H\in A^{N\times(N-k)}$}$ with the properties

is called a parity check matrix to the code $ \mbox{$C$}$.

If $ \mbox{$c\in C$}$ is a code word and $ \mbox{$e\in A^N$}$ the difference between the word obtained after transmission and the original code word, then the multiplication with the check matrix

$ \mbox{$\displaystyle (c+e)H\;=\;cH + eH\;=\;eH $}$
yields the syndrom $ \mbox{$eH$}$ of $ \mbox{$c+e$}$.

A MDD for a linear code $ \mbox{$C$}$ is defined by $ \mbox{$f:A^N\to C$}$ with $ \mbox{$f(a) = a - a'$}$ where $ \mbox{$a'$}$ depending on $ \mbox{$a$}$ is chosen such that $ \mbox{$a'H=aH$}$ and such that $ \mbox{$d(a',0) = \min\{d(x,0)\;:\; x\in A^N,\; xH = aH\}$}$.

(If $ \mbox{$\frac{d(C)-1}{2}$}$ is greater equal than the number of transmission errors (inside a transmitted code word) then one obtains by $ \mbox{$a = c+e$}$ as above $ \mbox{$a' = e$}$ .)

Binary Hamming Codes.

A binary Hamming Code of length $ \mbox{$N=2^r-1$}$ (with $ \mbox{$r\in\mathbb{N}$}$) is determined by a check matrix $ \mbox{$H\in\mathbb{F}_2^{N\times r}$}$ with the property that its row vectors are just all vectors of $ \mbox{$\mathbb{F}_2^r\backslash\{0\}$}$. Hamming codes are $ \mbox{$[N,N-r,3]$}$-Codes. The advantage for the practice is the simple error correction.

For binary Hamming codes and $ \mbox{$a\in\mathbb{F}_2^N$}$ the syndrom $ \mbox{$aH$}$ is at most at one position different from zero. The (unique) MDD is given by

$ \mbox{$\displaystyle f(a) = \begin{cases} a & \text{ provided } aH = (0,\dots, 0)\\ a - e_i & \text { in case } aH = i\text{-th row of } H, \end{cases}$}$
where $ \mbox{$e_i$}$ denotes the $ \mbox{$i$}$-th canonical vector of $ \mbox{$\mathbb{F}_2^N$}$. If there is more than one error during the transmission then decoding yields a wrong code word.

()

Examples:

[Links]
  automatically generated 7/ 7/2005