Mathematics-Online lexicon: Introduction to Finite Fields

	[home] [lexicon] [problems] [tests] [courses] [auxiliaries] [notes] [staff]
	Mathematics-Online lexicon:
	Introduction to Finite Fields

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z

overview

Rings and Fields

A Ring is a set with an addition $\mbox{$+$}$ and a multiplication $\mbox{$\cdot$}$ , which are both associative. The addition is commutative. Moreover the following law of distributivity holds in

$\displaystyle \forall a,b,c \in R : a \cdot (b + c) = a \cdot b + a \cdot c \ .$

Each ring has a zero element $\mbox{$0$}$ and a unity $\mbox{$1$}$ such that

$\displaystyle \forall a \in R : a + 0 = a$ and $\displaystyle a \cdot 1 = a \ .$

For each $\mbox{$x\in R$}$ exists $\mbox{$-x\in R$}$ such that $\mbox{$x + (-x) = 0$}$ .

If additionally for each element $\mbox{$x\in R\backslash \{ 0\}$}$ there is a multiplicative inverse $\mbox{$x^{-1}$}$ , i.e. $\mbox{$x\cdot x^{-1} = 1$}$ , then is called a skew field (or often also a division ring).

If the multiplcation is commutative, then a ring is called commutative and a skew field is called a field.

Examples.

The integers $\mbox{$\mathbb{Z}$}$ form with the usual addition and multiplication a commutative ring but not a field.
Examples for fields are the rational numbers $\mbox{$\mathbb{Q}$}$ , the real numbers $\mbox{$\mathbb{R}$}$ and the complex numbers $\mbox{$\mathbb{C}$}$ .
Quadratic $n \times n$ - matrices over $\mbox{$\mathbb{R}$}$ (or over any other field) form with matrix addition and matrix multiplication a ring. This ring is for $n \geq 2$ not commutative.
Let be a commutative ring. Then $\mbox{$R[X]$}$ denotes the polynomial ring over $\mbox{$R$}$ in the indeterminate $\mbox{$X$}$ . Its elements are polynomials with coefficients in $\mbox{$R$}$ . A typical element of has the form

$\displaystyle p(X) = a_0 + a_1X +a_2X^2 + \ldots +a_nX^n$
with $a_n \neq 0$ and $a_i \in R$ for $1\leq i \leq n .$ The index is called the degree of Addition and multiplication are the usual one for polynomials and with these operations is a commutative ring.

Note that a polynomial is a formal expression. It becomes a function from to by substituting by elements of For some rings $\mbox{$R$}$ it is possible that different polynomials of yield in this way the same function.

Ideals.

An ideal $\mbox{$I$}$ in a commutative ring $\mbox{$R$}$ is a subset of such that

$\mbox{$I + I\subseteq I$}$ .
$\mbox{$R\cdot I\subseteq I$}$ .

For example the even numbers $\mbox{$2\mathbb{Z}$}$ are an ideal of $\mbox{$\mathbb{Z}$}$ or $\mbox{$(X^2 + 1)\mathbb{R}[X]$}$ is an ideal of $\mbox{$\mathbb{R}[X]$}$ .

Each ideal $\mbox{$I$}$ of $\mbox{$R$}$ defines a new ring, the so-called residue class ring $\mbox{$R/I$}$ . The elements of are subsets of of the following form. Let be a fixed element of Then

$\displaystyle \overline {s} := \{x \in R ; x - s \in I \}$

is called the residue class of with respect to the ideal Note that $\overline {s} = \overline {t}$ if and only if $s \in \overline {t}$ if and only if $t \in \overline {s} .$ An element $x \in \overline {t}$ is called a representative of the residue class.

One checks easily that with the following addition and multiplication

$\displaystyle \overline {s} + \overline {t} := \overline {s+t} , \ \ \ \ \overline {s} \cdot \overline {t} := \overline {s \cdot t} .$

is a commutative ring.

Example. $\mbox{$\mathbb{Z}/2\mathbb{Z}$}$ has the elements $\mbox{$2\mathbb{Z}= \{\dots,-2,0,2,\dots\}$}$ and $\mbox{$1 + 2\mathbb{Z}= \{\dots,-1,1,\dots\}$}$ . The calculations in $\mbox{$\mathbb{Z}/2\mathbb{Z}$}$ may be done by representatives (omitting the bars and taking into account that ) ,

$\mbox{$\displaystyle 3\cdot (5 + 7) + 4 \; =\; 1\cdot (1 + 1) + 0 \; =\; 1\cdot 0 + 0 \; =\; 0\; , $}$

because modifications modulo $\mbox{$2\mathbb{Z}$}$ are permitted. More cumbersome but also correct is the calculation

$\mbox{$\displaystyle 3\cdot (5 + 7) + 4 \; =\; 40 \; =\; 0 . $}$

Finite Fields

We define first with the ideal $p\mathbb{Z}$ of $\mathbb{Z}$ the finite fields with elements, a prime, via

$\mbox{$\displaystyle \mathbb{F}_p := \mathbb{Z}/p\mathbb{Z}.$}$

Using the notation above the elements of are described by

$\displaystyle \overline {0}, \overline {1}, \ldots , \overline {p-1} .$

Note that $n\mathbb{Z}$ is for each natural number an ideal of $\mathbb{Z}.$ But the residue class ring $\mathbb{Z}/n\mathbb{Z}$ is a field if and only if is a prime. If is not a prime, then $n = a \cdot b$ with natural numbers $a, b \geq 2 .$ In $\mathbb{Z}/n\mathbb{Z}$ one gets $\overline {a} \cdot \overline {b} = \overline {0} .$ Hence neither $\overline {a}$ nor $\overline {b}$ are zero and both elements have no multiplicative inverse.

A polynomial $\mbox{$f(X) = X^k + a_{k-1} X^{k-1} + \cdots + a_0$}$ in $\mbox{$\mathbb{F}_p[X]$}$ is called irreducible, if it is not the product of two polynomials of lower degree. Otherwise it is called reducible. The irreducible polynomials play in $\mathbb{F}_p[X]$ a similar role as the primes in $\mathbb{Z}.$ Note that irreducibility quite often may be checked only by testing all possible divisors of a given polynomial , i.e. by division of by any polynomial of degree less or equal than a half of the degree of

Examples.

${$\mbox{$X^2 + 1\in\mathbb{F}_3[X]$}$}$ is irreducible. If it would be reducible then a linear factor (i.e. a polynomial of degree 1) $\mbox{$X - a$}$ would be a divisor. Consequently $\mbox{$a$}$ would be a zero of the polynomial. But $\mbox{$X^2 + 1$}$ has no zeros in $\mbox{$\mathbb{F}_3$}$ .
$\mbox{$X^2 + 1\in\mathbb{F}_2[X]$}$ is reducible because $\mbox{$X^2 + 1 = (X + 1)\cdot (X + 1)$}$ .
In $\mathbb{F}_2(X)$ the polynomial is reducible. But it has no zero in $\mathbb{F}_2 .$

Using irreducible polynomials over the field of elements one can construct all other finite fields. This is the main content of the following theorem.

Theorem.

${$\mbox{$f(X) = X^k + a_{k-1} X^{k-1} + \cdots + a_0$}$}$ is irreducible if and only if
$\mbox{$\displaystyle \mathbb{F}_{p^k} := \mathbb{F}_p[X]/f(X)\mathbb{F}_p[X]$}$
is a field.
If and are different irreducible polynomials of degree , then the fields $\mathbb{F}_p[X]/r(X)\mathbb{F}_p[X]$ and $\mathbb{F}_p[X]/q(X)\mathbb{F}_p[X]$ are isomorphic.
For each prime $\mbox{$p$}$ and for each $\mbox{$k\geq 1$}$ exists an irreducible polynomial of degree $\mbox{$k$}$ in $\mbox{$\mathbb{F}_p[X]$}$ .
There is up to isomorphism precisely one finite field with elements. (This justifies the notation ${$\mbox{$\mathbb{F}_{p^k}$}$}$ .)
The number of elements of a finite field is of prime power order

The constant polynomials form with addition and multiplication in $\mbox{$\mathbb{F}_p\subseteq \mathbb{F}_{p^k}$}$ a field ( more precisely a subfield of $\mathbb{F}_{p^k}$ ) which is obviously isomorphic to $\mathbb{F}_p .$ .

Let and be polynomials in $\mbox{$\mathbb{F}_p[X]$}$ such that $1 \leq$ deg $f(X) \leq$ deg $\ g(X) .$ . Then by polynomial division we can write

$\mbox{$\displaystyle g(X)\; =\; t(X) f(X) + r(X) \; , $}$

where the degree of the residue $\mbox{$r(X)$}$ is less than the degree of $\ g(X) .$ Thus in $\mbox{$\mathbb{F}_{p^k}$}$

$\mbox{$\displaystyle g(X)\; =\; r(X) \; . $}$

Suppose that $\mathbb{F}_{p^k} = \mathbb{F}_p[X]/g(x)\mathbb{F}_p(X)$ with irreducible polynomial

$\displaystyle g(X) = X^k + a_{k-1} X^{k-1} + \cdots + a_0) - (a_{k-1} X^{k-1} + \cdots + a_0 .$

Then we can express in $\mathbb{F}_{p^k}$ as

$\mbox{$\displaystyle X^k \; =\; 1\cdot(X^k + a_{k-1} X^{k-1} + \cdots + a_0) ... ..._{k-1} X^{k-1} + \cdots + a_0) \; =\; - (a_{k-1} X^{k-1} + \cdots + a_0)\; . $}$

Using this one shows that each element of $\mathbb{F}_{p^k}$ may be expressed as a unique linear combination of of the elements $1, X , X^2, \ldots , X^{k-1}$ over $\mathbb{F}_p .$ So $\mbox{$\mathbb{F}_{p^k}$}$ is a vector space over $\mbox{$\mathbb{F}_p$}$ with basis $\mbox{$\{1,X,X^2,\dots,X^{k-1}\}$}$ .

A vector space of dimension $\mbox{$k$}$ over $\mbox{$\mathbb{F}_p$}$ has $\mbox{$p^k$}$ elements. Therefore $\mbox{$\mathbb{F}_{p^k}$}$ has $\mbox{$p^k$}$ elements and these elements are represented by all polynomials of degree less than

Note that the residue class ring $\mbox{$\mathbb{Z}/p^k\mathbb{Z}$}$ has also $\mbox{$p^k$}$ elements. But for $\mbox{$k\geq 2$}$ this ring is not a field because then is not a prime (see above). Also in $\mbox{$x\in\mathbb{F}_{p^k}$}$ the equation

$\mbox{$\displaystyle \underbrace{x + x + \cdots + x}_{p\;\text{ summands}} = 0$}$

is valid for each element. This is for $1 \in$ $\mathbb{Z}$ /p^k $\mathbb{Z}$

not the case.

Primitive Elements, Zech-Logarithms

Each element in $\mbox{$x$}$ of $\mbox{$\mathbb{F}_{p^k}\backslash\{0\}$}$ staisfies the equation $\mbox{$x^{p^k-1} = 1$}$ . If $\mbox{$p^k-1$}$ is the minimal exponent $\mbox{$m \geq 1$}$ such that $\mbox{$x^m =1 $}$ then is called primitive.

One can show that each finite field has at least one primitive element. Note that if $\alpha$ is primitive, then each non-zero element of $\mathbb{F}_{p^k}$ is a power of $\alpha .$ Note that a randomly chosen element of a finite field is with high probability primitive.

Fix a primitive element primitive element $\mbox{$\alpha\in\mathbb{F}_{p^k} .$}$ Then with respect to this element Zech-logarithms are defined as follows.

If $\mbox{$1 + \alpha^m = \alpha^l$}$ then $\mbox{$l\in [1,p^k - 2]$}$ is called the Zech-logarithm of $\mbox{$m\in [0,p^k - 2]$}$ . Note that $\mbox{$l$}$ is uniquely determined except in the case when $\mbox{$\alpha^m = -1$}$ . In this case we define $\mbox{$l = -1$}$ .

All non -zero elements of a finite field are described by a power of a primitive element. Thus multiplications of these elements may be easily performed. The Zech-logarithms are useful for the addition, because for $\mbox{$\alpha^j\neq -\alpha^i$}$

$\mbox{$\displaystyle \alpha^i + \alpha^j\; =\; \alpha^i (1 + \alpha^{j-i}) \; =\; \alpha^{i + l}\; , $}$

where $\mbox{$l$}$ denotes the Zech-logarithm of $\mbox{$j - i$}$ . In the case $\mbox{$\alpha^j = -\alpha^i$}$ the formula does not apply. But in this case the result is

Example. Consider the field of elements defined as $\mbox{$\mathbb{F}_4 := \mathbb{F}_2[X]/(X^2 + X + 1)\mathbb{F}_2[X]$}$ . $\alpha = X$ is primitive, because $\mbox{$\alpha^1 = X$}$ , $\mbox{$\alpha^2 = X + 1$}$ and $\mbox{$\alpha^3 = 1$}$ . The corresponding Zech - logarithms follow from the the table

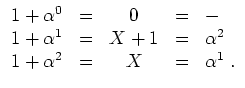
$\mbox{$\displaystyle \begin{array}{rcccl} 1 + \alpha^0 & = & 0 & = & - \\ 1... ... & = & \alpha^2 \\ 1 + \alpha^2 & = & X & = & \alpha^1\; . \\ \end{array}$}$

The Zech - logarithm of $\mbox{$m = 0$}$ is $\mbox{$l = -1$}$ and $\mbox{$\alpha^1 + \alpha^2 = \alpha(1 + \alpha^1) = \alpha^{1 + 2} = 1$}$ .

Frobenius Automorphism

The Frobenius-automorphism of $\mbox{$\mathbb{F}_{p^k}$}$ is a bijective map $F: \mathbb{F}_{p^k} \longrightarrow \mathbb{F}_{p^k}$ defined by

$\mbox{$\displaystyle F(x) = x^p$}$

It has the properties that

$\displaystyle F(xy) = F(x)F(y) \$ and $\displaystyle \ \ F(x+y) = F(x) + F(y) \$ for $\displaystyle x,y \in \mathbb{F}_{p^k}.$

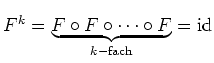Because for $a \in \mathbb{F}_p$ ( $\mathbb{F}$ _p considered as subfield), it follows that $\mbox{$F(ay) = a F(y)$}$ provided $\mbox{$a\in\mathbb{F}_p$}$ . Clearly $x^{p^k} = x$ for a primitive element of $\mathbb{F}_{p^k} .$ Therefore this equation is valid for each element of $\mathbb{F}_{p^k}$ and it follows for the Frobenius automorphism that $\mbox{$F^k = \underbrace{F\circ F\circ \cdots\circ F}_{k-\text{fach}} = {\mbox{id}}$}$ .

(Author: Kimmerle)

Examples:

Algebraische Konstruktion der komplexen Zahlen (german)
Nullabbildung im Körper mit 3 Elementen (german)

[Links]

automatically generated 7/ 7/2005