Mo logo [home] [lexicon] [problems] [tests] [courses] [auxiliaries] [notes] [staff] german flag
Mathematics-Online course: Basic Mathematics - Complex Numbers

Circle in the Gaussian Plane

[previous page]   [table of contents][page overview]
The equation

$\displaystyle \vert z-a\vert = s \vert z-b\vert,\quad s\ne 1\, , $

describes a circle in the Gaussian plane. Its center is

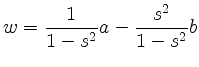
$\displaystyle w=\frac{1}{1-s^2}a-\frac{s^2}{1-s^2}b $

and the radius given by

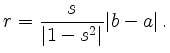
$\displaystyle r=\frac{s}{\vert 1-s^2\vert}\vert b-a\vert \,. $

If $ s< 1$, $ a$ is located in the interior of the circle, while $ b$ is lies on its outside, vice versa for $ s > 1$.

\includegraphics[width=10cm]{kreis_komplexe_ebene}

The circle's parametric representation is given by

$\displaystyle w + r e^{\mathrm{i}t},\quad t\in[0,2\pi) \,. $

(Authors: Höllig/Kopf/Abele)

(temporary unavailable)
Interpreting the equation

$\displaystyle \vert z-a\vert = s \vert z-b\vert,\quad s\ne 1\, , $

geometrically, it asserts that the distances of a point $ Z$ from two given points $ A$ and $ B$ have a fixed ratio $ s$, i.e.,

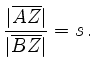
$\displaystyle \frac{\vert\overline{AZ}\vert}{\vert\overline{BZ}\vert}=s\,. $

In order to determine the points for which this relationship holds, we consider, e.g., the case $ s<1$, and use the following auxiliary construction.

\includegraphics[width=10cm]{kreis_des_apollonius}

Referring to the figure, we denote by $ Z_i$ and $ Z_a$ the points on the line $ AB$ with

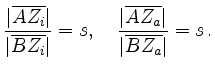
$\displaystyle \frac{\vert\overline{AZ_i}\vert}{\vert\overline{BZ_i}\vert}=s,\quad \frac{\vert\overline{AZ_a}\vert}{\vert\overline{BZ_a}\vert}=s \,. $

Moreover, we define two points $ S_1$ and $ S_2$ as the intersections of the line parallel to $ BZ$ through $ A$ with the line $ g$ through $ Z$ and $ Z_i$ and the line $ h$ through $ Z$ and $ Z_a$, respectively. Then it follows from the intercept theorem that

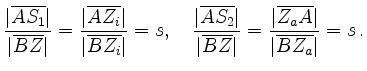
$\displaystyle \frac{\vert\overline{AS_1}\vert}{\vert\overline{BZ}\vert}= \frac{... ...e{BZ}\vert}= \frac{\vert\overline{Z_aA}\vert}{\vert\overline{BZ_a}\vert}=s \,. $

Since $ \vert\overline{AZ}\vert\,:\,\vert\overline{BZ}\vert=s$ as well, the line segments $ \overline{AZ}, \overline{AS_1}$ and $ \overline{AS_2}$ have the same length. Moreover, $ g$ and $ h$ are orthogonal. Hence, $ Z_a$, $ Z$, $ Z_i$ form a right triangle, and all points $ Z$ fulfilling these requirements are located on the circle with diameter $ \overline{Z_aZ_i}$.

This geometric argument is due to Apollonius (200 BC), which is why such a circle is called an Apollonius circle.

(Authors: Hörner/Abele )

(temporary unavailable)
[previous page]   [table of contents][page overview]
  automatically generated 10/31/2008