Mathematics-Online problems: Lösung zu: Problem 451: Indefinite Integration

	[home] [lexicon] [problems] [tests] [courses] [auxiliaries] [notes] [staff]
	Mathematik-Online problems: Lösung to
	Problem 451: Indefinite Integration

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z

Find the following indefinite integrals

Recall the simple power integration rule,

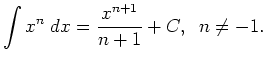
$\displaystyle \int x^n \; d x = \frac{x^{n+1}}{n+1} + C, \;\; n \ne -1.$

(a)

$\displaystyle \int \frac{10}{\sqrt[5]{x}} \; d x$

Rewrite the expression as

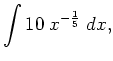$\displaystyle \int \frac{10}{\sqrt[5]{x}} \; d x$	$\displaystyle =$	$\displaystyle \int 10 \; x^{-\frac{1}{5}} \; d x,$
	$\displaystyle =$	$\displaystyle 10 \int x^{-\frac{1}{5}} \; d x,$
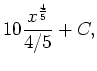	$\displaystyle =$	$\displaystyle 10 \frac{x^{\frac{4}{5}}}{4/5} + C,$
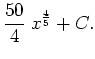	$\displaystyle =$	$\displaystyle \frac{50}{4} \; x^{\frac{4}{5}} + C.$

(b)

$\displaystyle \int (x+1)(2x-5) \; \ud x$

By expanding the polynomial, the power integration rule can easily be applied.

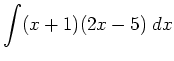$\displaystyle \int (x+1)(2x-5) \; d x$	$\displaystyle =$	$\displaystyle \int (2x^2-5x+2x-5) \; d x,$
	$\displaystyle =$	$\displaystyle \int (2x^2-3x-5) \; d x,$
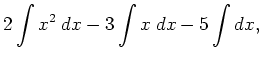	$\displaystyle =$	$\displaystyle 2\int x^2 \; d x -3 \int x \; d x -5 \int d x,$
	$\displaystyle =$	$\displaystyle 2 \frac{x^3}{3} -3 \frac{x^2}{2} -5x + C.$

(c)

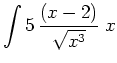
$\displaystyle \int 5 \, \frac{(x-2)}{\sqrt{x^3}} \; \ud x$

Rewrite the expression as

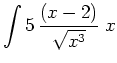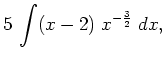$\displaystyle \int 5 \, \frac{(x-2)}{\sqrt{x^3}} \; \ud x$	$\displaystyle =$	$\displaystyle 5 \, \int (x-2) \; x^{-\frac{3}{2}} \; d x,$
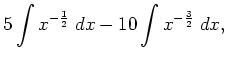	$\displaystyle =$	$\displaystyle 5 \int x^{-\frac{1}{2}} \; d x -10 \int x^{-\frac{3}{2}} \; d x,$
	$\displaystyle =$	$\displaystyle 5 \; \frac{x^{\frac{1}{2}}}{1/2} -10 \; \frac{x^{-\frac{1}{2}}}{-1/2} + C,$
	$\displaystyle =$	$\displaystyle 10 \; x^{\frac{1}{2}} + 20 \; x^{-\frac{1}{2}} + C,$
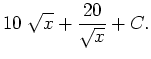	$\displaystyle =$	$\displaystyle 10 \; \sqrt{x} + \frac{20}{\sqrt{x}} + C.$

(Author: Rafee )

automatisch erstellt am 14. 10. 2004