

Mathematics-Online course: Preparatory Course Mathematics - Analysis - Extrema and Curve Sketching

|
[home] [lexicon] [problems] [tests] [courses] [auxiliaries] [notes] [staff] |

|
|
Mathematics-Online course: Preparatory Course Mathematics - Analysis - Extrema and Curve Sketching | ||
Curve Sketching | ||
| [previous page] [next page] | [table of contents][page overview] |
![\includegraphics[width=14.5cm]{Kurvendiskussion_en.eps}](/inhalt/aussage/aussage45/img2.png)
Symmetry:
Since
![]() , the function is odd.
, the function is odd.
Periodicity:
As the sine function, the function is ![]() -periodic.
Hence, it is sufficient to consider the interval
-periodic.
Hence, it is sufficient to consider the interval
![]() .
.
Points of discontinuity and Poles: The function is a composition of continuous functions, and, therefore, has no points of discontinuity or poles.
Zeros:
By the addition theorem,
![]() ,
and it follows that
,
and it follows that
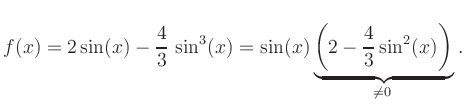
Extrema: The derivative

Inflection Points: The second derivative
Asymptots:
Since ![]() is periodic and not constant, it has no asymptotes.
is periodic and not constant, it has no asymptotes.
![\includegraphics[width=10.4cm]{Kurvendiskussion_1_en}](/inhalt/beispiel/beispiel45/img28.png)
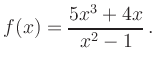
Symmetry: The numerator is even and the denominator is odd. Thus the function is odd, i.e., symmetric with respect to the origin.
Periodicity: The function is not periodic.
Points of Discontinuity and Poles:
The denominator of ![]() has simple zeros at
has simple zeros at ![]() .
Since the numerator is nonzero at these points, the singularities are not
removable and hence
.
Since the numerator is nonzero at these points, the singularities are not
removable and hence ![]() and
and ![]() are simple poles.
are simple poles.
Zeros:
The nominator vanishes at ![]() .
.
Extrema: The derivative
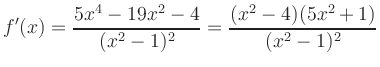
Inflection Points: The second derivative
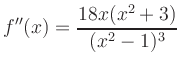
Asymptotes: Polynomial division yields
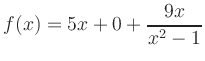
![\includegraphics[width=10.4cm]{Kurvendiskussion_2_en}](/inhalt/beispiel/beispiel46/img21.png)
(i) Qualitative behavior:
As the exponential function, ![]() does not possess any symmetries and is not
periodic.
does not possess any symmetries and is not
periodic.
The derivative is discontinuous at ![]() in view of the discontinuity of
the absolute value at the argument 0.
Since
in view of the discontinuity of
the absolute value at the argument 0.
Since
![]() for all
for all ![]() ,
,
![]() is the asymptote to
is the asymptote to ![]() for
for
![]() .
For
.
For
![]() an asymptote does not exist since
an asymptote does not exist since
![]() .
.
(ii) Zeros:
In view of the positivity of the exponential function,
the zeros of ![]() are determined by the first factor und equal
are determined by the first factor und equal
![]() .
Since
.
Since ![]() , the zeros are also global minima.
A global maximum does not exist since
, the zeros are also global minima.
A global maximum does not exist since
![]() .
.
(iii) Extrema:
Since
![]() ,
the intervals
,
the intervals ![]() and
and
![]() each contain at least one local maximum.
Differentiating
each contain at least one local maximum.
Differentiating
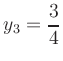 e
e(iv) Inflection points: The zeros of
![\includegraphics[width=10.4cm]{Kurvendiskussion_3_en}](/inhalt/beispiel/beispiel47/img35.png)
| [previous page] [next page] | [table of contents][page overview] |
| automatically generated 1/9/2017 |