Mo logo [home] [lexicon] [problems] [tests] [courses] [auxiliaries] [notes] [staff] german flag
Mathematics-Online course: Vector Calculus - Quadratic Curves

Ellipse

[previous page] [next page] [table of contents][page overview]
For the points $ P=(x,y)$ on an ellipse the sum of the distances from two fixed points $ F_{\pm}$ (the foci) is a given positive constant:

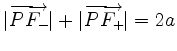
$\displaystyle \vert\overrightarrow{PF_-}\vert + \vert\overrightarrow{PF_+}\vert = 2 a $

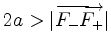with $ 2a>\vert\overrightarrow{F_-F_+}\vert$ .

\includegraphics[width=12.4cm]{a_ellipse}

If $ F_{\pm}=(\pm f,0)$ , then we have for the coordinates

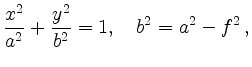
$\displaystyle \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1,\quad b^2 = a^2 - f^2\, , $

and

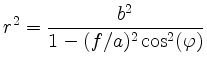
$\displaystyle r^2 = \frac{b^2}{1-(f/a)^2\cos^2(\varphi)} $

for the polar coordinates of the points $ P$ .

A parameterisation of the ellipse is given by

$\displaystyle x=a\cos t,\quad y=b\sin t $

with $ t\in [0,2\pi)$ .

Equivalence of the representations follows immediatly by calculation.

To proof

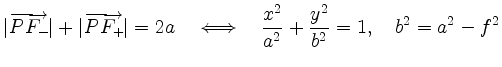
$\displaystyle \vert\overrightarrow{PF_-}\vert + \vert\overrightarrow{PF_+}\vert... ...{\displaystyle{\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1}},\quad b^2 = a^2 - f^2 $

by squaring of

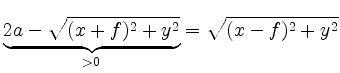
$\displaystyle \underbrace{2a - \sqrt{(x+f)^2 + y^2}}_{> 0} = \sqrt{(x-f)^2 + y^2} $

we obtain the equivalent equation

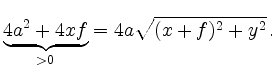
$\displaystyle \underbrace{4a^2 + 4xf}_{>0} = 4a \sqrt{(x+f)^2 + y^2}\, . $

Squaring again and dividing by $ 4a$ yield

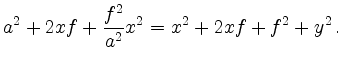
$\displaystyle a^2 + 2xf + \frac{f^2}{a^2} x^2 = x^2 + 2xf + f^2 + y^2\, . $

Substituting $ f^2 = a^2-b^2$ and transforming we obtain the coordinate form.

To proof

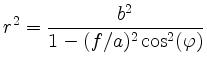
$\displaystyle r^2 = \frac{b^2}{1-(f/a)^2\cos^2(\varphi)} $

we multiply by the denominator and take into account that

$\displaystyle x^2 = (x^2 + y^2)\cos^2(\varphi)\, . $

This implies

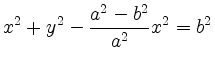
$\displaystyle x^2 + y^2 - \frac{a^2-b^2}{a^2} x^2 = b^2 $

and division by $ b^2$ yields the coordinate form.

[previous page] [next page] [table of contents][page overview]
  automatically generated 10/30/2007