Mo logo [home] [lexicon] [problems] [tests] [courses] [auxiliaries] [notes] [staff] german flag
Mathematics-Online course: Basic Mathematics - Real Numbers

Bernoulli's Inequation

[previous page] [next page] [table of contents][page overview]

For $ x \in \mathbb{R}$ with $ x > -1$ and $ n \in \mathbb{N}_0$,

$\displaystyle 1 + nx \leq (1+x)^n \,. $

(Authors: Kimmerle/Abele)

The inequality can be proved via induction.

For $ n = 0$ the assertion obviously is correct:

$\displaystyle 1 + 0x = 1 = (1+x)^0 \,. $

Let us suppose the assertion holds for an $ n\in\mathbb{N}$. Then we have

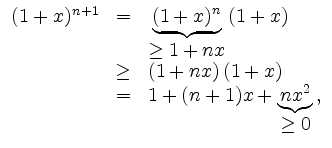
$\displaystyle \begin{array}{rcl} (1+x)^{n+1} & = & \underbrace{(1+x)^n}_{\displ... ... & = & 1+(n+1)x + \underbrace{nx^2}_{\displaystyle \geq 0} \,, \\ \end{array}$

and thus the assertion also follows for the exponent $ n+1$.
(Authors: Kimmerle/Abele)
[previous page] [next page] [table of contents][page overview]
  automatically generated 10/31/2008