

Mathematics-Online course: Basic Mathematics - Real Numbers

|
[home] [lexicon] [problems] [tests] [courses] [auxiliaries] [notes] [staff] |

|
|
Mathematics-Online course: Basic Mathematics - Real Numbers | ||
Rational Numbers | ||
| [previous page] [next page] | [table of contents][page overview] |
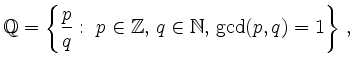
As is illustrated in the figure,
![]() is countable.
With the so-called diagonal method, we can
enumerate all positive fractions.
Uncancelled fractions are skipped in the count.
is countable.
With the so-called diagonal method, we can
enumerate all positive fractions.
Uncancelled fractions are skipped in the count.
Finally, the rational numbers form a dense subset of the real line. Between any two different rational numbers there are infinitely many rational numbers.
| [previous page] [next page] | [table of contents][page overview] |
| automatically generated 10/31/2008 |