

Mathematics-Online course: Linear Algebra - Analytic Geometry - Quadrics

|
[home] [lexicon] [problems] [tests] [courses] [auxiliaries] [notes] [staff] |

|
|
Mathematics-Online course: Linear Algebra - Analytic Geometry - Quadrics | ||
Quadratic Form | ||
| [previous page] [next page] | [table of contents][page overview] |
Dependent on the sign of the
eigenvalues of ![]() we distinguish
between three types:
we distinguish
between three types:
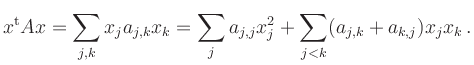
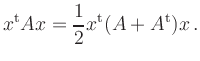
Quadratic forms occur, for example, in the
Taylor expansion of a scalar function ![]() :
:
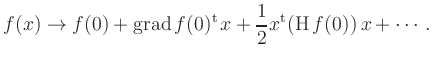
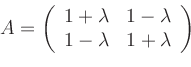
Hence, the quadratic form
| automatically generated 4/21/2005 |