

Mathematics-Online course: Linear Algebra - Normal Forms - Singular Value Decomposition

|
[home] [lexicon] [problems] [tests] [courses] [auxiliaries] [notes] [staff] |

|
|
Mathematics-Online course: Linear Algebra - Normal Forms - Singular Value Decomposition | ||
Topography | ||
| [previous page] [next page] | [table of contents][page overview] |
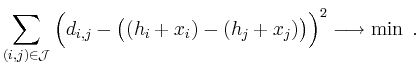
>> h=[834, 561, 207, 9]'; >> d=[276, 631, 822, 356, 549]';where
Let
![$\displaystyle A:=
\left[\begin{array}{rrrr} 1 & -1 & 0 & 0 \\ 1 & 0 & -1 & 0 \\ 1 & 0 & 0 & -1
\\ 0 & 1 & -1 & 0 \\ 0 & 1 & 0 & -1 \end{array} \right]$](/inhalt/beispiel/beispiel229/img7.png) and
andSV-decomposition of matrix A:
>> A=[1 -1 0 0 ; 1 0 -1 0 ; 1 0 0 -1 ; 0 1 -1 0 ; 0 1 0 -1];
>> [U,S,V]=svd(A)
U =
0.5774 0.4082 -0.0000 -0.7071 -0.0000
0.5774 -0.2041 -0.5000 0.3536 0.5000
0.5774 -0.2041 0.5000 0.3536 -0.5000
-0.0000 -0.6124 -0.5000 -0.3536 -0.5000
-0.0000 -0.6124 0.5000 -0.3536 0.5000
S =
2.0000 0 0 0
0 2.0000 0 0
0 0 1.4142 0
0 0 0 0.0000
0 0 0 0
V =
0.8660 0 0 -0.5000
-0.2887 -0.8165 0.0000 -0.5000
-0.2887 0.4082 0.7071 -0.5000
-0.2887 0.4082 -0.7071 -0.5000
Computation of the pseudo inverse
![]() by means of the
by means of the
![]() -matrix
-matrix ![]() the entries of which are
the entries of which are
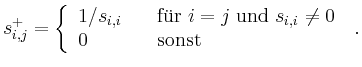
>> SP=diag(1./diag(S(1:3,1:3)));
>> SP(4,5)=0
SP =
0.5000 0 0 0 0
0 0.5000 0 0 0
0 0 0.7071 0 0
0 0 0 0 0
>> AP=V*SP*U'
AP =
0.2500 0.2500 0.2500 -0.0000 -0.0000
-0.2500 0.0000 0.0000 0.2500 0.2500
-0.0000 -0.3750 0.1250 -0.3750 0.1250
0.0000 0.1250 -0.3750 0.1250 -0.3750
Solving the approximation problem
by multiplying the right hand side ![]() by the pseudo inverse
by the pseudo inverse ![]() :
:
>> x=AP*(d-A*h)
x =
1.0000
-1.0000
-3.0000
3.0000
Remark: The pseudo inverse can directly be computed by the MATLAB-command pinv.
| automatically generated 4/21/2005 |