

Mathematics-Online lexicon: Annotation to

|
[home] [lexicon] [problems] [tests] [courses] [auxiliaries] [notes] [staff] |

|
|
Mathematics-Online lexicon: Annotation to | ||
Binomial Theorem | ||
| A B C D E F G H I J K L M N O P Q R S T U V W X Y Z | overview |
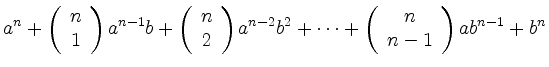 |
|||
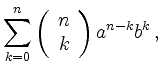 |
In particular, for ![]() , the formula yields
, the formula yields
The binomial theorem can be proved via mathematical induction.
For ![]() and
and ![]() the equation holds because of
the equation holds because of
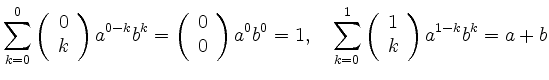
Let us now assume that
the equation holds for ![]() . This yields
. This yields
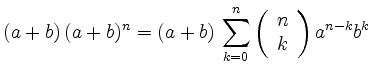 |
|||
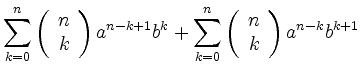 |
|||
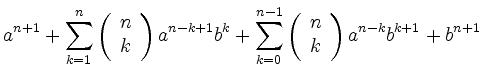 |
|||
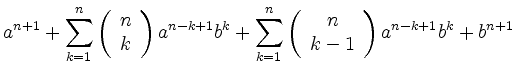 |
|||
![$\displaystyle a^{n+1} + \sum_{k=1}^n \left[
\left( \begin{array}{c} n \\ k \end...
...eft( \begin{array}{c} n \\ k-1 \end{array}\right)\right]
a^{n+1-k}b^k + b^{n+1}$](/inhalt/erlaeuterung/erlaeuterung40/img13.png) |
|||
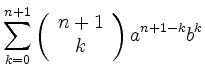 |
| automatisch erstellt am 11. 6. 2007 |