Mo logo [home] [lexicon] [problems] [tests] [courses] [auxiliaries] [notes] [staff] german flag
Mathematics-Online lexicon:

Real Fourier-Series

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z overview
The real Fourier series of a real $ 2\pi$-periodic function $ f$ is an orthogonal expansion in terms of sines and cosines:

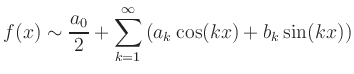
$\displaystyle f(x) \sim \frac{a_0}{2} + \sum_{k=1}^\infty \left( a_k\cos(kx)+b_k\sin(kx)\right) $

with

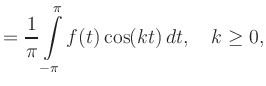$\displaystyle a_k$ $\displaystyle = \frac{1}{\pi} \int\limits_{-\pi}^\pi f(t)\cos(kt)\,dt,\quad k\ge0,$    
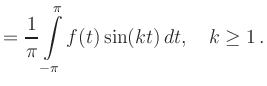$\displaystyle b_k$ $\displaystyle = \frac{1}{\pi} \int\limits_{-\pi}^\pi f(t)\sin(kt)\,dt,\quad k\ge1\,.$    

The type and rate of convergence of the series depends on the smoothness of $ f$. For example, sufficient for absolute convergence is that the series $ \sum_{k=0}^\infty \vert a_k\vert$ and $ \sum_{k=1}^\infty \vert b_k\vert$ converge.

A convergent Fourier series needs not to represent the true function value at every point. Usually, at a point of discontinuity, the series converges to the arithmetic mean of the left and right limits of $ f$. This explains the notation $ f(x) \sim \sum \cdots$ instead of $ f(x)= \sum \cdots$, which emphasizes these convergence issues.

[Examples] [Links]
  automatically generated 9/22/2016