Mo logo [home] [lexicon] [problems] [tests] [courses] [auxiliaries] [notes] [staff] german flag
Mathematics-Online lexicon:

Algorithmic error

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z overview

Let

$\displaystyle x_i = \varphi_i(x_j,x_k,\ldots),\quad i=m+1,\ldots,n, $

denote a sequence of operations which compute a final output value $ x_n$ from input values $ x_1,\ldots ,x_m$. For such an algorithm, the error $ \Delta x_n=\tilde{x}_n-x_n$ of the numerically computed result $ \tilde{x}_n$ satisfies

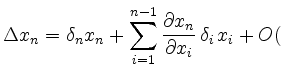$\displaystyle \Delta x_n =\delta_n x_n + \sum_{i=1}^{n-1} \frac{\partial x_n}{\partial x_i}\, \delta_i\, x_i+O($eps$\displaystyle ^2) $

with $ \vert\delta_i\vert\le$eps.

The partial derivatives $ \displaystyle\frac{\partial x_n}{\partial x_i}$ control the influence of the errors $ \delta _i x_i$ on the output value $ x_n$. The corresponding amplification factors for the absolute relative errors $ \vert\delta_i x_i\vert/\vert x_i\vert$ are the so- called condition numbers

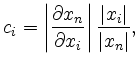
$\displaystyle c_i=\left\vert\frac{\partial x_n}{\partial x_i}\right\vert\frac{\vert x_i\vert}{\vert x_n\vert}, $

and

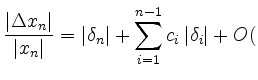$\displaystyle \frac{\vert\Delta x_n\vert}{\vert x_n\vert}=\vert\delta_n \vert + \sum_{i=1}^{n-1} c_i\,\vert\delta_i\vert+O($eps$\displaystyle ^2) $

for $ x_n \neq 0$.

We say that the algorithm defined by the operations $ \varphi_{m+1},\ldots ,\varphi_n$ is stable if intermediate errors are not substantially more amplified than relative errors of the input values, i.e. if

$\displaystyle \max _{m<i<n}c_i\leq \gamma \max _{1\leq i\leq m}c_i $

with $ \gamma$ not too large.

Annotation:

[Examples] [Links]
  automatically generated 3/ 8/2007